Кинетические исследования ферментативных реакций необходимы не только для количественного определения ферментов и сравнения скоростей их функционирования, но, в еще большей степени, для расшифровки механизмов ферментативных реакций. В этих целях, прежде всего, необходимо уметь корректно вычислять кинетические параметры ферментативных реакций, оценивать конкурентный или неконкурентный характер действия ингибиторов. Рассмотрим основные уравнения, описывающие ферментативную кинетику и способы вычислений. Основное внимание будет уделено не строгости математического вывода уравнений, а правильному их использованию для получения достоверных результатов.

При выводе кинетических уравнений количественно характеризующих ферментативную активность, обычно делают следующие допущения.

1. Фермент и субстрат образуют фермент-субстратный комплекс за счет сил физической природы. Из этого комплекса в дальнейшем освобождаются фермент и продукт. Таким образом, химической реакцией является только второй этап – распад фермент-субстратного комплекса:

2. Концентрация субстрата обычно значительно выше концентрации фермента. Поэтому при рассмотрении начальных скоростей реакции, когда

3. Константа диссоциации определяется соотношением:

концентрация продукта очень низка, обратимостью второй стадии можно пренебречь. Следовательно, – const., а скорость образования продукта равна:

Поскольку общая концентрация фермента равна сумме концентраций свободного фермента и фермента, связанного в комплекс, то + или = –.

Подставляя значение [Е] = [Е0] — [ES] из (4), получаем:

С другой стороны, из уравнения следует:

В уравнении выражение к+2 можно рассматривать как максимальную скорость, достигаемую, когда концентрация фермент-субстратного комплекса численно равна общей концентрации фермента. Следовательно:

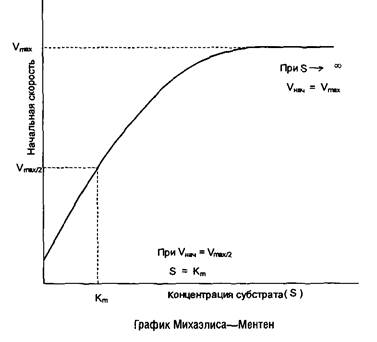
Выражение есть не что иное, как уравнение Михаэлиса–Ментен для ферментативной кинетики, а величина Кга = Ks представляет собой меру сродства фермента к субстрату. Численно она равна такой концентрации субстрата, при которой начальная скорость ферментативной реакции составляет половину максимальной скорости. Уравнение графически выражается гиперболой.

Для практического определения кинетических параметров этот график неудобен, к тому же требует использования концентраций субстрата, «насыщающих» фермент, что не всегда достижимо при ограниченной растворимости субстрата. Поэтому обычно стремятся преобразовать уравнение Михаэлиса–Ментен в такую форму, чтобы графически оно изображалось прямой линией. Чаще всего для этого используют метод Лайнуивера–Берка, представляя уравнение Михаэлиса–Ментен в виде уравнения прямой линии:

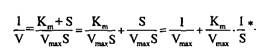
Последнее выражение называют уравнением Лайнуивера–Берка и для расчета кинетических параметров используют график, построенный в координатах: 1/V против 1/S. В результате получается прямая, отсекающая на оси ординат отрезок, равный 1/V, а на продолжении оси абсцисс отрезок, равный – 1/Кга. Однако следует отметить, что при использовании графика Лайнуивера–Берка точки в области высоких концентраций субстрата располагаются слишком густо, а положение прямой линии во многом зависит от точек в области низких концентраций субстрата, где определение скорости менее надежно. Кроме того, реальные экспериментальные данные не всегда адекватно аппроксимируются в виде прямой линии.

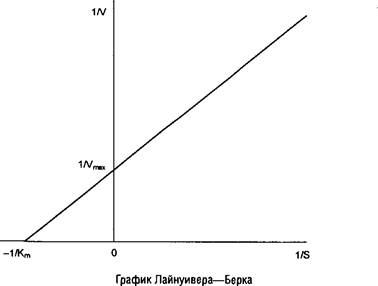
Поэтому предложено еще несколько приемов для определения кинетических параметров. Метод Эди–Хофсти также основан на преобразовании уравнения Михаэлиса–Ментен. Умножив обе части уравнения на и преобразовав, получим:

График этого уравнения в координатах V против V/S представляет собой прямую линию, отсекающую на осях ординат и абсцисс отрезки, равные VmaxH Vm>x/ Кго соответственно.

Прочие статьи:

Экономическое значение хрящевых рыб
Большинство видов хрящевых рыб не образует плотных скоплений, что затрудняет их добычу. Поэтому объектами специального промысла служат лишь немногие виды и в ограниченных районах. Значительно чаще многие виды хрящевых рыб добываются попут ...

Торможение
Торможение — в физиологии — активный нервный процесс, вызываемый возбуждением и проявляющийся в угнетении или предупреждении другой волны возбуждения. Обеспечивает (вместе с возбуждением) нормальную деятельность всех органов и организма ...

Ближайшие предки человека
Третичный период по сравнению со всей историей человека длился чрезвычайно долго. Начался он около 70 млн. и закончился примерно 1 млн. лет тому назад. Значение третичного периода в истории Земли, особенно её животного и растительного ми ...