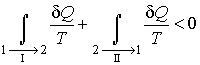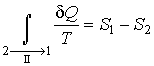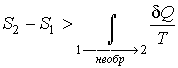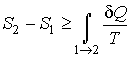Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 1.

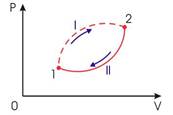
Рис.1. Необратимый круговой термодинамический процесс

Пусть процесс будет необратимым, а процесс - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид

Так как процесс является обратимым, для него можно воспользоваться соотношением (3.53) , которое дает

Подстановка этой формулы в неравенство (3.55) позволяет получить выражение

Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство

в котором знак равенства имеет место в случае, если процесс является обратимым, а знак больше, если процесс - необратимый.

Неравенство (3.58) может быть также записано и в дифференциальной форме

Если рассмотреть адиабатически изолированную термодинамическую систему, для которой , то выражение (3.59) примет вид

или в интегральной форме

Прочие статьи:

Описать механизм и условия, необходимые для образования условного рефлекса. Начертить схему рефлекторной дуги
Условные рефлексы – это рефлексы, которые легко приобретаются в течение жизни и образуются на основе безусловного рефлекса при действии условного раздражителя (свет, звук, время и т.д.) Механизм образования условного рефлекса состоит в ус ...

Цитоархитектоника и миелоархитектоника новой коры
В соответствии с делением полушарий на пять долей выделяют пять основных областей – лобную, теменную, височную, затылочную и островковую, имеющие различия в строении и выполняющие разные функции. Однако общий план строения новой коры один ...

Сельскохозяйственное использование
Телорез. Стебли этого растения поднялись со дна в большом количестве и зеленым ковром покрыли поверхность озера. Телорез широко распространен в озерах, старицах и прудах области. Сначала растение развивается под водой. Весной от избытка у ...